Motion estimation
Motion compensation is used extensively in video processing, where it constitutes an essential enabling technology for meeting quality expectations in the multiformat digital delivery world. But not every technology in the motion-compensated category delivers equal quality, a fact of increasing significance as more processes requiring motion compensation are concatenated in the video distribution chain.
It is common for a signal to pass through three or more compression stages and two or more conversion stages before it reaches the viewer. Each process is motion-compensated, none are lossless, and all introduce their own set of artifacts. The higher the quality of the motion estimators in the concatenated signal chain, the better the overall picture quality delivered to the viewer.
Broadly speaking, there are three main types of motion estimation: block matching, gradient and phase correlation.
Block matching
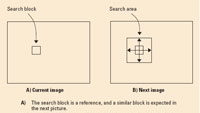
In block matching, an image on the screen is divided into a grid of blocks. (See Figure 1.) One block of the image is compared a pixel at a time with a block in the same place in the next image. If there is no motion, there is a high correlation between the two blocks.
If something has shifted, the same place position in the next field will not provide good correlation, and it will be necessary to search for the best correlation in the next image. The position that gives the best correlation is assumed to be the new location of a moving object.
Block matchers work at the pixel level, so they are poor at tracking larger objects and high-motion speeds. To overcome this, hierarchical techniques are used, where block matching is initially carried out with large blocks. Then the process is repeated at subdivided blocks all the way down to pixel resolution.
Get the TV Tech Newsletter
The professional video industry's #1 source for news, trends and product and tech information. Sign up below.
Such hierarchical techniques try to balance the ability to track large objects versus small objects. In practice, however, they fall short on accuracy when tracking small, fast-moving objects, such credit roll text. They also tend to introduce spurious motion vectors on cuts, fades, sources with noise and other irregular material.
Gradient
The gradient method is based on analyzing the relationship between the spatial and temporal luminance gradients, where the spatial luminance gradient is a property of the current image, and the temporal luminance gradient is the gradient between successive images.
This technique showed great promise when first adopted on professional equipment in the early 1990s, and it performs well for processing relatively clean, continuous video feeds. It runs into problems, however, in the real world of irregular moving pictures, where the technique may mistake a different object in the next frame for a spatial gradient.
Phase correlation
Phase correlation is the most powerful and accurate motion estimation technique for video processing. It is also the most technologically sophisticated, and an understanding of how it works requires some familiarity with frequency domain analysis and the use of Fourier transforms.
The main principle behind phase correlation is the shift theory. (See Figure 2.) In the shift theory, a simple single sine wave is sampled at different times, t = 0 and t = +1. In the interval between these two points in time, the sine wave has moved, but there is more than one way to represent this movement. It can be understood as a displacement of 20 pixels or as a phase difference of 45°. Shift theory shows that the displacement in the time domain equates to the phase shift in the frequency domain.
While this is easy to grasp when dealing with a single sine wave, TV signals are obviously more complex. For this reason, a Fourier transform needs to break down the waveform of the video signal into a series of sine waves. (See Figure 3.) In this instance, a square wave pattern is broken down into sine waves. For each sine wave, the phase is provided. If the phase information is available from successive images, the motion can be measured.
This principle is the basis for the complete phase correlation system shown in Figure 4. Spectral analysis is performed on two successive fields, and then all of the individual phase components are subtracted. The phase differences are then subjected to a reverse transform. The outputs of the reverse transform provide a correlation surface that contains peaks, the position of which corresponds to the motion between successive images.
The phase correlation system is highly accurate. One aspect of this accuracy is its sensitivity to the effects of variations in noise and lighting, which ensures high-quality performance on fades, objects moving in and out of the shade, and flashes of light.
Motion estimation applications
Motion estimation technology is used for several video processing tasks, including deinterlacing, SD-to-HD upconversion and HD-to-HD conversion. All of these require temporal interpolation to enable full-resolution, artifact-free outputs. The main benefit of reducing artifacts is, of course, a cleaner and more pleasing picture for the viewer. However, artifact elimination also simplifies subsequent compression and decompression processes, as less processing power is wasted on noise.
Within the compression systems themselves, motion estimation technology plays a fundamental role in exploiting temporal redundancy. For the same level of output quality, non-motion-compensation methods are limited to a compression ratio of 5:1, whereas motion compensation allows compression ratios of 100:1.
Deinterlacing
Many viewers watch television on flat-screen displays that use progressive scan technology. Most video, however, is still acquired and transmitted using the interlaced scan technology created for CRTs in the 1930s. The ability to deinterlace video with minimal artifacts is a key video processing technique. Beyond its significance as a discrete process, deinterlacing is also a key step in standards conversion and SD-to-HD upconversion.
Interlacing video can be understood as a primitive form of compression. For a 480-line NTSC display, it sends 240 odd lines and then 240 even lines 16 milliseconds later. Thanks to persistence of vision, this is sufficient to create the illusion of moving pictures without requiring all 480 lines to be sent with each field.
The problem in converting interlaced video to a progressive scan, in which the 480 lines are drawn on the screen sequentially from top to bottom, is that the interlaced fields were sampled at different points in time. Unless the picture is entirely static, there has been motion between the two fields.
One way to convert interlaced video to progressive format is to merely filter out either all the odd or all the even fields, but this would reduce the resolution of the image by half. Motion-adaptive processing techniques preserve full resolution for the static areas of the picture, but still throw away half the resolution for the moving parts of the image.
Only motion compensation can convert interlaced video to progressive without losing any resolution on both the stationary and moving parts of the picture. By calculating motion vectors, it is able to recreate the missing lines from an interlaced scan. Thus, it restores each field to its full resolution.
However, there are several ways to perform motion compensation, and not all deliver the same level of vector reliability and precision. The highest level of vector reliability and precision is obtained by phase correlation, which analyzes incoming images and shifts the pixels in each video field so that they line up perfectly, even for complex scenes where there is fast motion, fine graphics or mixed film and video material.
Standards conversion and upconversion
Standards conversion is another genre of video processing that benefits from motion compensation and phase correlation. The benefits are clear if we consider that the component parts of the standards conversion process are deinterlacing, frame rate conversion and scaling.
The frame-rate conversion process benefits from the accurate and reliable motion vectors of phase-correlation motion compensation for the same reason that deinterlacing benefits. The difference, in the case of 50Hz to 60Hz conversion, is that the technique replaces 50 frames of video with 60 frames of video, each of which are sampling different points in time within the same one-second interval.
Consider, then, the challenges of performing this kind of processing on a pixel-by-pixel basis between formats of HD video, where the bandwidth is five times higher than SD, and there are five times the number of vectors to be calculated with five times the precision. The HD-to-HD conversion process involves a minimum of 16-bit resolution with 3Gb/s data rates throughout, and more advanced picture building techniques are required to deal with the issues associated with revealed and obscured areas of the image.
At the same time, the screens on which HD video is watched tend to be larger, making artifacts much more obvious than on the typical SD screen. For such applications, phase-correlation motion compensation technology is capable of delivering outputs that are artifact-free, low in noise, and high in detail and fidelity.
The future
Motion compensation technology was once only available in high-end broadcast products, but over the last decade, it has begun to trickle down into higher-volume commodity products. This technology migration will continue, and we can expect that high-end algorithms will find their way into display devices and consumer-grade software.
Certainly motion compensation will continue to be a key technology block in the future, even as it advances from today's 2-D applications to 3-D motion vectors that describe not only horizontal and vertical motion but also give an accurate measurement of depth, or Z-plane motion. With this added dimension, and with further increases in picture resolution to come, the possibilities for advanced high-efficiency algorithms will be virtually unlimited.
Joe Zaller is vice president of strategic marketing for Snell & Wilcox.
